重读统计学习方法:Bagging与Boosting
决策树模型是很基础的模型,之后的很长时间里,学术届在它基础上扩展出了集成学习的概念,也就是耳熟能详的Bagging模型和Boosting模型。前者将多个决策树的预测结果取投票/均值作为最终的预测结果,构成了随机森林模型,后者通过顺序训练树,每个新树专注于修正前面所有树汇总后的残差,最终通过加权求和输出结果。
Bagging与随机森林

随机森林的思想主要是想通过组合多个决策树来提高模型性能。这是因为单棵树很容易过拟合,即方差太大,所以需要多颗树来进行平衡。因此这也决定了在构建随机森林时,子树之间不能太像,即树之间的协方差要低,从公式上来看: $\mathrm{Var}(\hat{f}) = \frac{1}{T} \mathrm{Var}(\text{单棵树}) + \left(1 - \frac{1}{T}\right) \mathrm{Cov}(\text{树}_i, \text{树}_j)$
为了降低不同树之间的方差,随机森林的办法是:数据随机和特征随机。前者用Bootstrap实现,后者用特征随机选择实现。
Bootstrap抽样
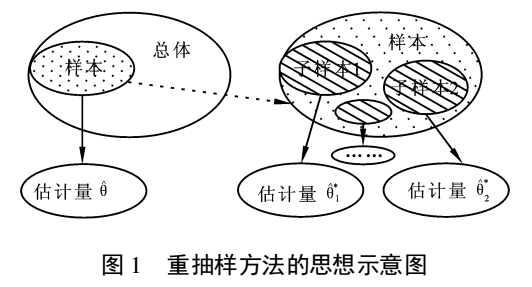
Bootstrap出现的很早,核心思想是通过重抽样,有放回的抽取子样本来模拟总体分布,从而估计整体分布。这么做有几点好处,首先它不要求数据满足特定分布,不像t检验和z检验要求满足正态分布。
其次,多次有放回抽样也可以满足小样本的场景,抽样产生了的虚拟样本量足够估计数据的分布。并且,多次重复抽样可以让异常值和噪音的干扰弱化。
特征随机选择
随机森林在子树分裂时,并不是选的全量特征,而是从中随机选部分特征。每次分裂节点时,都随机选择子特征,使得一些弱特征不会被频繁过滤。同一棵树的不同节点可能关注不同的特征组合。例如,某节点可能关注“年龄”和“收入”,而下一节点可能关注“性别”和“职业”。
之所以每次选部分子特征,是因为在实验中,每次使用全量特征,会导致模型准确率下降。对于特征子集大小的选择,当特征子集过小(只有一个特征)时,单棵树的预测能力下降,偏差提高,当特征子集过大时,每个子树就都变成了普通决策树,也失去了Bagging的意义,方差提高。
工业实现
随机森林的优势在于多颗树可以并行训练,这使得它在早期工业界很流行,不过在分布式场景还是有很大的优化空间。主要的思路在数据存储和特征分裂上,以Spark为例,Spark MLlib版本的随机森林用RDD和分区存储数据,这是数据层面的优化,在训练优化上,集群上的每个Worker独立获取随机数据训练树。特征分裂时也同样如此,每个Worker独立的找特征的最佳分裂点。
以下内容摘自github
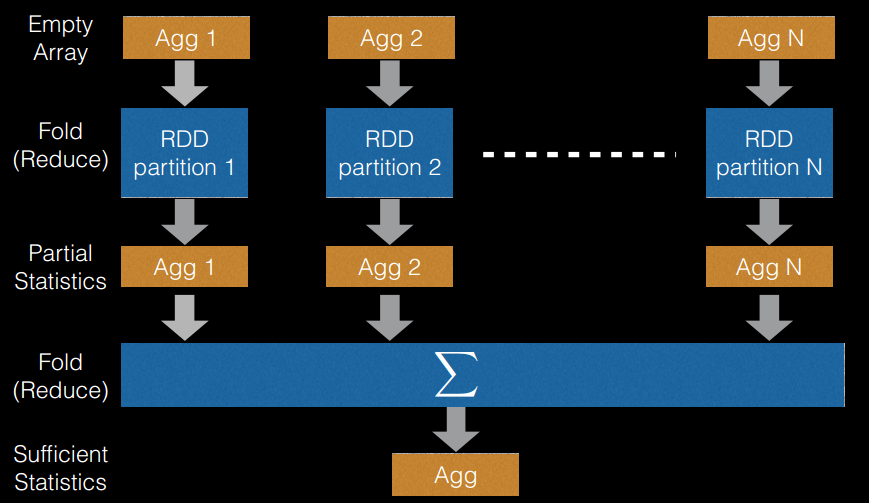
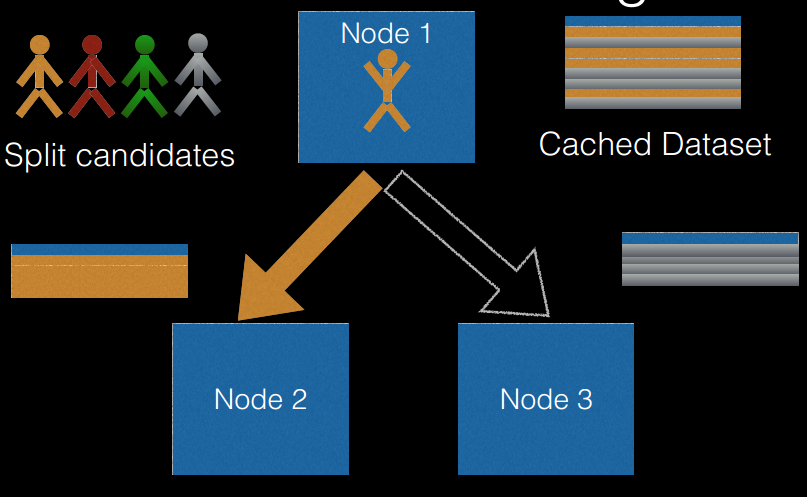
- 切分点抽样统计,如下图所示。在单机环境下的决策树对连续变量进行切分点选择时,一般是通过对特征点进行排序,然后取相邻两个数之间的点作为切分点,这在单机环境下是可行的,但如果在分布式环境下如此操作的话, 会带来大量的网络传输操作,特别是当数据量达到
PB级时,算法效率将极为低下。为避免该问题,Spark中的随机森林在构建决策树时,会对各分区采用一定的子特征策略进行抽样,然后生成各个分区的统计数据,并最终得到切分点。 (从源代码里面看,是先对样本进行抽样,然后根据抽样样本值出现的次数进行排序,然后再进行切分)。
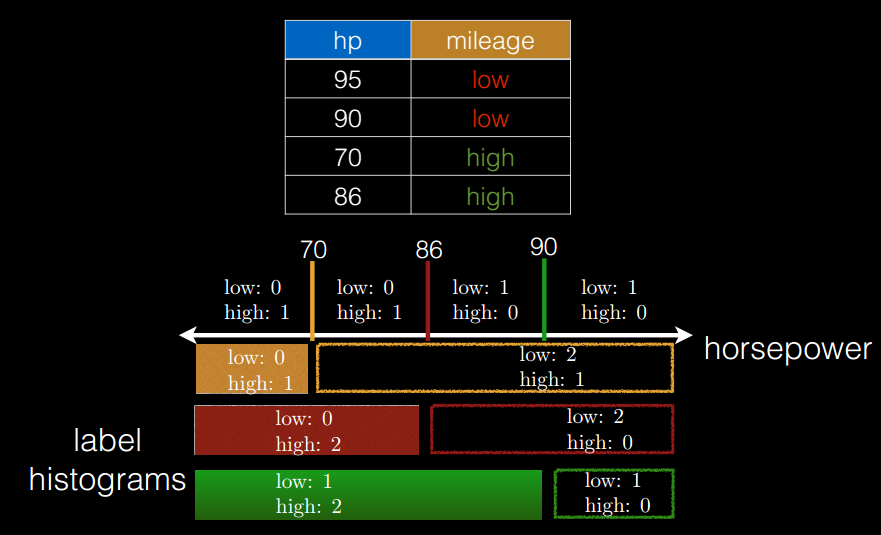
- 特征装箱(
Binning),如下图所示。决策树的构建过程就是对特征的取值不断进行划分的过程,对于离散的特征,如果有M个值,最多有2^(M-1) - 1个划分。如果值是有序的,那么就最多M-1个划分。 比如年龄特征,有老,中,少3个值,如果无序有2^2-1=3个划分,即老|中,少;老,中|少;老,少|中。;如果是有序的,即按老,中,少的序,那么只有m-1个,即2种划分,老|中,少;老,中|少。 对于连续的特征,其实就是进行范围划分,而划分的点就是split(切分点),划分出的区间就是bin。对于连续特征,理论上split是无数的,在分布环境下不可能取出所有的值,因此它采用的是切点抽样统计方法。
- 逐层训练(
level-wise training),如下图所示。单机版本的决策树生成过程是通过递归调用(本质上是深度优先)的方式构造树,在构造树的同时,需要移动数据,将同一个子节点的数据移动到一起。 此方法在分布式数据结构上无法有效的执行,而且也无法执行,因为数据太大,无法放在一起,所以在分布式环境下采用的策略是逐层构建树节点(本质上是广度优先),这样遍历所有数据的次数等于所有树中的最大层数。 每次遍历时,只需要计算每个节点所有切分点统计参数,遍历完后,根据节点的特征划分,决定是否切分,以及如何切分。
Boosting与Adaboost
Boosting模型的核心思想是用新的学习器,拟合当前学习器的残差,来逐步降低误差。这个思想来自于历史上的一个概念:如果存在一个多项式算法能够学习一个预测类,并且正确率很高,那么就是强可学习,而如果这个算法学习后的正确率只比随机猜好,那就是弱可学习。再后来,强可学习被证明和弱可学习是等价的,也就是说,一个弱可学习的算法在理论上可以不断提升到强可学习。
另一方面,弱学习算法比直接得到强学习算法要更简单,因此提升方法就希望通过组合多个弱学习器来构成一个强学习器。体现这一思想的算法有很多,比较早的是Adaboost。
Adaboost
同样是预测残差,Adaboost本身还有一个样本权重的机制,权重的目的是为了区分较难学习的样本和较易学习的样本。在第一轮训练中,每个样本被赋予相同的权重。假设数据集有$N$个样本,初始化权重为$w_i^{(1)} = \frac{1}{N} \quad (i = 1, 2, \dots, N)$
随后训练第一个弱分类器,并在预测后统计错误样本的加权误差率。这个误差率里用到了前面初始化的样本权重,并用来计算这个弱分类器的权重,误差越低,权重越高。这个分类器权重的公式是$\alpha_t = \frac{1}{2} \ln\left( \frac{1 - \epsilon_t}{\epsilon_t} \right)$。
第一个分类器处理完以后,更新样本权重,其中错误样本的权重被提高,$w_i^{(t+1)} = \frac{w_i^{(t)} \cdot e^{-\alpha_t y_i h_t(x_i)}}{Z_t}$,其中${Z_t}$是归一化因子,用来调整权重和为1。
开始训练第二个弱分类器,并同样更新样本权重和分类器权重,以此类推。当模型训练完以后,最终的预测结果是所有弱分类器的加权投票。
AdaBoost算法优点:
- 利用弱分类器进行级联
- 可以用不同的算法作为弱分类器
- 充分考虑每个分类器的权重,这和Bagging是不一样的
Adaboost算法缺点:
- AdaBoost迭代次数也就是弱分类器数目不太好设定
- 数据不平衡会导致分类精度下降
- 训练比较耗时,每次需要重新选择当前分类器的最优切分点
2025/3/16 于苏州