特征工程：类别变量除了独热编码还有什么编码？

在学习机器学习的过程中，在学习各式各样的模型前，数据预处理往往是我们最先开始学习的部分。这部分内容看起来没有各式各样的模型那样抓人眼球，但是在整个机器学习流程中扮演着非常重要的角色。有一句经典的话：“数据质量决定上限，而模型只是逼近这个上限。”

在刚开始打Kaggle的那段时间，我只用过Label Encoding和OneHot Encoding。这两个编码方式各有优劣，我的理解是，Label Encoding适合有序分类。OneHot Encoding适合无序分类，但会让维度线性增长。一个场景就是地点特征，如果一个分类中有五十个城市，独热编码会带来五十个维度，而标签编码会为不同城市带来错误的位置信息。

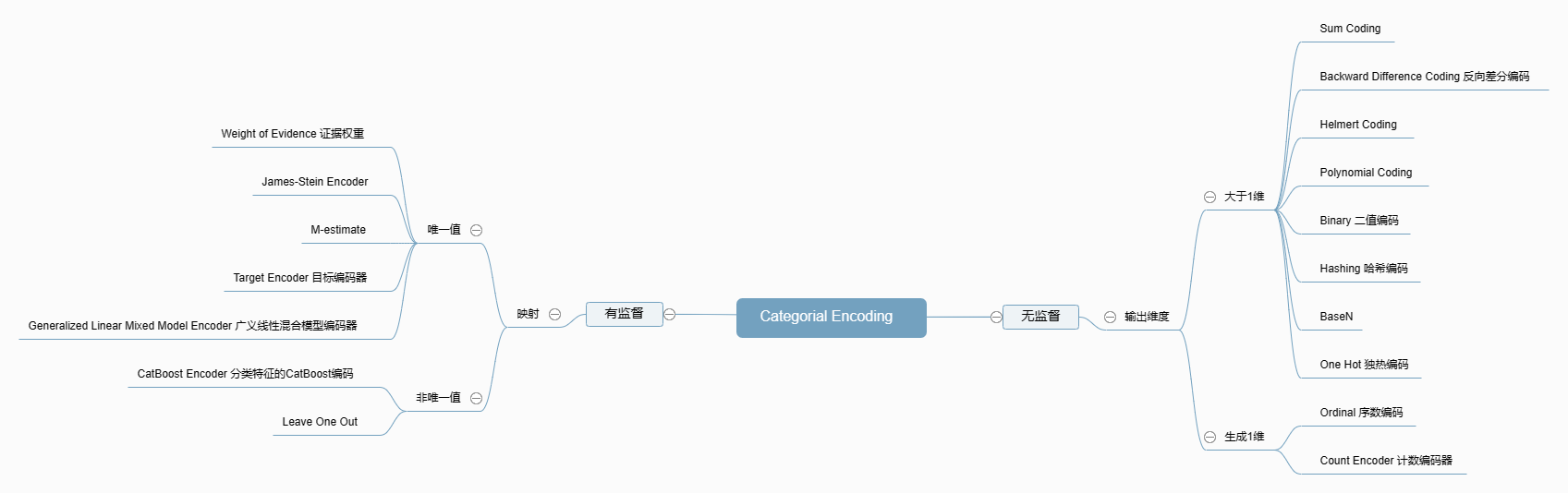
显然这两种编码方式不足以应付所有的场景，因此有必要接触和学习一下新的编码方式。Python中的Category Encoders库封装了22种编码方式，今天来解读一下。

Ordinal Encoding

首先是Ordinal Encoding，序列编码。这种编码针对的是有序的标签，例如学历，等级等等。对于一个具有 𝑚 个类别的特征，我们将其对应地映射到 [0,𝑚−1] 的整数。

这样做的好处是，比Label Encoder处理的标签增加了类别之间的等级/数值关系。缺点是不能处理无序标签，而且类别之前的距离关系也不够精确。

代码实现：

import numpy as np
import pandas as pd
import category_encoders as ce

data = {
    'CustomerID': [1, 2, 3, 4, 5],
    'Satisfaction': ['Satisfied', 'Dissatisfied', 'Neutral', 'Satisfied', 'Dissatisfied'],
    'ProductType': ['Electronics', 'Furniture', 'Electronics', 'Clothing', 'Furniture']
}

X = pd.DataFrame(data)

encoder = ce.OrdinalEncoder(cols=['Satisfaction', 'ProductType'], return_df=True)
numeric_dataset  = encoder.fit_transform(X)

除了这种方式，也可以直接用map方法来映射：

1 2	`ord_map = {'Gen 1': 1, 'Gen 2': 2, 'Gen 3': 3, 'Gen 4': 4, 'Gen 5': 5, 'Gen 6': 6} df['Category_Label'] = df['Category_Label'].map(ord_map)`

Count Encoding/Frequency Encoding

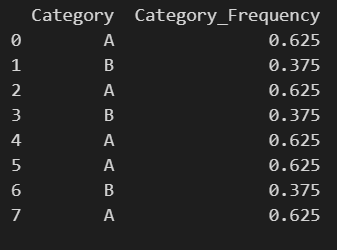
下一个编码方式是频数编码，即将类别特征替换为在数据集中出现的次数。假如某个特征出现了100次，那么就记作100。

这种编码方式适合高基数的数据集，也就是类别数特别多。在前面提到的多城市场景，它可以作为一种编码方式，来体现城市的热门程度。不过它只考虑类别自身出现的次数，不考虑类别之间的关系，会丢失一定的信息。此外，不同类别的出现次数可能一致，这也会带来一定的混淆。

import pandas as pd

data = {'Category': ['A', 'B', 'A', 'B', 'A', 'A', 'B', 'A']}
df = pd.DataFrame(data)

frequency_map = df['Category'].value_counts(normalize=True).to_dict()
#frequency_map = df.groupby('Category').size()/len(df)
df['Category_Frequency'] = df['Category'].map(frequency_map)

print(df[['Category', 'Category_Frequency']])

import category_encoders as ce

data = {
    'CustomerID': [1, 2, 3, 4, 5],
    'Satisfaction': ['Satisfied', 'Dissatisfied', 'Neutral', 'Satisfied', 'Dissatisfied'],
    'ProductType': ['Electronics', 'Furniture', 'Electronics', 'Clothing', 'Furniture']
}

X = pd.DataFrame(data)

encoder = ce.CountEncoder(cols=['Satisfaction', 'ProductType'], return_df=True)
numeric_dataset  = encoder.fit_transform(X)

Binary Encoding/Hash Encoding/Base N Encoding

我把二进制编码，哈希编码和BaseN编码放在了一起，因为它们都是只是将类别进行映射。

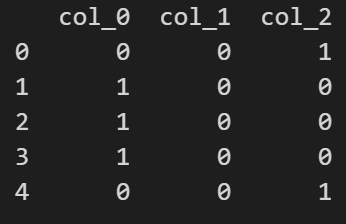
二进制编码分为两步：先为每个类别分配ID，再根据ID生成对应的二进制编码。本质上是用二进制对ID进行哈希映射。

哈希编码也是类似，字符串将被转换为一个惟一的哈希值。对于稀疏的高维特征，可以使用哈希编码。

BaseN编码则是将类别编码为Base-N代表的数组，N越高代表输出的维度越高。

import pandas as pd
import category_encoders as ce

data = {
    'Color': ['Red', 'Blue', 'Green', 'Blue', 'Red']
}

X = pd.DataFrame(data)

encoder = ce.HashingEncoder(n_components=3)
numeric_dataset = encoder.fit_transform(X['Color'])

print(numeric_dataset)

Target Encoding

目标编码，对于每个类别，计算该类别下目标变量的均值，或者其他统计量（中位数等等）。这是一种有监督的编码方式。如果直接使用均值，可能会过拟合，在更普适的情况下，利用样本的先验概率和后验概率结合权重函数来得到均值，其中还会进行一些贝叶斯平滑。

data = {
    'CustomerID': [1, 2, 3, 4, 5],
    'Satisfaction': ['Satisfied', 'Dissatisfied', 'Neutral', 'Satisfied', 'Dissatisfied'],
    'ProductType': ['Electronics', 'Furniture', 'Electronics', 'Clothing', 'Furniture'],
    'Target': [1, 0, 0, 1, 0] 
}

df = pd.DataFrame(data)

X = df[['CustomerID', 'Satisfaction', 'ProductType']]
Y = df['Target']

encoder = ce.TargetEncoder(cols=['Satisfaction', 'ProductType'], min_samples_leaf=10, smoothing=1.0)
numeric_dataset = encoder.fit_transform(X, Y)

numeric_dataset

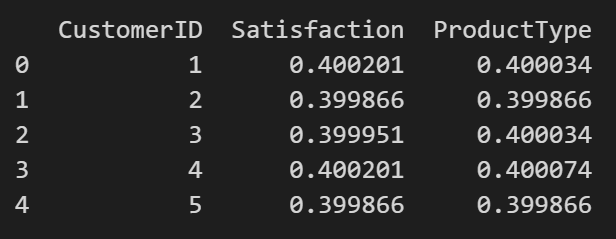
基于Target Encoding的思想，衍生出了不同的编码方式。

CatBoost Encoding

和Target Encoding思想类似，CatBoost Encoding使用目标变量的统计数据（如平均值）来替换每个类别，区别在于CatBoost 编码采取了特殊的策略来降低目标泄露（target leakage）和过拟合的风险。公式如下：$\text{Encoded value} =\frac{\text{TargetSum} + \text{prior}}{\text{FeatureCount} + 1} \tag{1}$。

Target Sum：指定类别在Target Value中的总和。找到所有类别为目标类别的行，计算它们对应的Target的和。
Prior：对于整个数据集而言，Target值的总和/所有的观测变量数目。这个值是固定的，即数据的行数/Target的总和。
FeatureCount：到目前为止已经看到的、具有与此相同值的分类特征的总数。+1防止分母为0。

例如，对于 color=["red", "blue", "blue", "green", "red", "red", "black", "black", "blue", "green"] and target column with values, target=[1, 2, 3, 2, 3, 1, 4, 4, 2, 3]。

这里，先验$\text{prior}=25/10=2.5$。

对于分类red，$\text{TargetSum}=1+3+1=5$，而red在特征中出现了3次。因此$\text{FeatureCount}=3$ 。所以最后编码为：$(5+2.5)/(3+1)=1.875$。

M Estimator Encoding

M Estimator Encoding是Target Encoding的简化版本。用于在保留类别之间差异的同时，通过引入全局均值来减少每个类别中的方差。它在处理具有少量样本的类别时比较有效。公式如下：

$\text{Encoded value} = \frac{n \times \text{mean}(y_{\text{category}}) + m \times \text{mean}(y_{\text{global}})}{n + m}$。

$n$ 是当前类别中的样本数量。
$\text{mean}(y_{\text{category}}) $是当前类别的目标均值。
$\text{mean}(y_{\text{global}})$ 是全数据集的目标均值。
$m$ 是一个平滑参数，它决定了全局均值在编码中的权重，值越大，编码值越倾向于全局均值。

import category_encoders as ce

data = {
    'Color': ['Red', 'Blue', 'Green', 'Blue', 'Red'],
    'Outcome': [1, 0, 1, 0, 1] 
}

df = pd.DataFrame(data)
encoder = ce.MEstimateEncoder(cols=['Color'], m=5.0)  

df_encoded = encoder.fit_transform(df['Color'], df['Outcome'])
print(df_encoded)

Leave One Out

Leave One Out也是基于目标编码，不过在传统的目标编码中，类别的编码值通过计算该类别中所有样本的目标变量均值获得。因为当前样本的目标值也参与了编码值的计算，可能会导致过拟合。留一编码通过对每个样本进行编码时排除该样本的目标值，来减少这种过拟合的风险。

公式如下：$\mu_{x_i}^{(-i)} = \frac{\sum_{j \neq i} y_j \cdot \mathbb{I}(x_j = x_i)}{\sum_{j \neq i} \mathbb{I}(x_j = x_i)}$

公式表示为为类别$x_i$的样本中，排除第$i$个样本后的目标变量均值。

分子部分：计算类别为$x_i$的样本中，排除第$i$个样本后的目标变量之和。

分母部分：计算类别为$x_i$的样本中，排除第$i$个样本后的样本数量。

$\mathbb{I}(x_j = x_i)$是指示函数，$x_j = x_i$时取值为1，否则为0。

这种情况下，当类别中目标值不同时，留一编码值会有所变化。

import category_encoders as ce

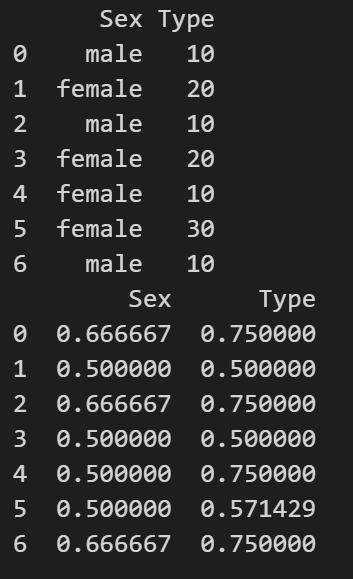
X = pd.DataFrame(np.array([['male',10],['female', 20], ['male',10], 
                       ['female',20],['female',10],['female',30],['male',10]]),
             columns = ['Sex','Type'])
y = np.array([0,1,1,0,1,0,1])
print(X)

encoder = ce.LeaveOneOutEncoder(cols = ['Sex', 'Type']).fit(X,y)
print(encoder.transform(X))

WoE

证据权重（Weight of Evidence）是关于分类自变量和因变量之间关系的编码方式。源自信用评分领域，曾用于区分用户是违约拖欠还是已经偿还贷款。证据权重的数学定义是优势比的自然对数，即：$\text{WoE} = \log\left(\frac{\text{Non-Events or Goods}}{\text{Events or Bads}}\right)$。

Non-Events or Goods ：在某个特定组或桶中好客户的比例。
Events or Bads ：在同一个组或桶中坏客户的比例。

如果一个分类变量的某个类别中有 20% 是坏客户（events），80% 是好客户（non-events），那么该类别的 WoE 计算为：

$\text{WoE} = \ln\left(\frac{\text{Proportion of Non-Events}}{\text{Proportion of Events}}\right) = \ln\left(\frac{80%}{20%}\right) = \ln(4)$

这个值表明该类别相对于其他类别在区分好坏客户上的强度。WoE 值越高，表明在该组中的好客户（non-events）的比例远高于坏客户（events）。这意味着该组的风险较低，或者说该组对于预测目标变量（比如违约）是有利的。WoE值越低（特别是负值），表示该组中坏客户的比例高于好客户。这意味着该组的风险较高，或者说该组对于预测目标变量是不利的。WoE为0，则这个组中的分布是完全随机的，预测能力完全不够。

WoE的问题在于没有考虑到变量之间的相关性，也只是从自身特征出发。此外，它只适用于二分类问题。

data = {
    'CustomerID': [1, 2, 3, 4, 5],
    'Satisfaction': ['Satisfied', 'Dissatisfied', 'Neutral', 'Satisfied', 'Dissatisfied'],
    'ProductType': ['Electronics', 'Furniture', 'Electronics', 'Clothing', 'Furniture'],
    'Target': [1, 0, 0, 1, 0]  
}

df = pd.DataFrame(data)
target = df['Target']

woe_encoder = ce.WOEEncoder()

df_encoded = woe_encoder.fit_transform(df[['Satisfaction', 'ProductType']], target)
print(df_encoded)

总结

离散特征的类别数过多的情况不宜使用OneHot Encoder，容易维度爆炸。
Target Encoder容易过拟合，因此需要加入CV，正则项。可以考虑使用Leave One Out。
对于有序离散特征，可以尝试使用OrdinalEncoder，BinaryEncoder，OneHotEncoder，LeaveOneOutEncoder，TargetEncoder。
对于回归问题，TargetEncoder和LeaveOneOutEncoder效果可能一般。
如果离散特征高基数，可以用LeaveOneOutEncoder，WOEEncoder，MEstimateEncoder。

2024/5/19 于苏州

数据挖掘

#数据挖掘 #特征工程 #机器学习

工程实践：高计算量的Python程序状态监测上一篇

分布式训练：了解Deepspeed中的ZeRO1/2/3 下一篇