博弈论:基本概念
博弈论是我从22年底就在断断续续看的东西,这个部分的内容是我根据斯坦福博弈论公开课,冯诺依曼的博弈论以及一些网络资源的理解得到的结论,因此理解上可能有所偏差。
今天早上打2v2斗地主的时候,碰到对面两个人均70万豆的土豪(原谅我们没见过世面,账户上的豆从来没超过十万:P),刚好这一局我们炸弹不少,等到最后双方只有几十张牌的时候,倍数已经叠到好几万了。这时候,记牌器显示对面还有8张10,而我们一个人手上有一个6张的2的炸弹,另一个人手上有2张2。
这时我们面临一个选择,这8张10是在一个人手上,还是每个人各4张?如果是前者,那我们如果选择炸掉,那输的时候,倍数就会翻倍,而如果是后者,那我们就稳赢了。基于他们是大土豪,他们是不是有很大的概率前面一直不出炸弹,而是留到最后?从他们的角度,我们俩个加起来才1万6的豆子,即使输,收益也不会输很多,因此会不会想着放我们走?
最后我们飞快打出炸弹,赢下了这一局,爽吃1万6的豆。这个过程无疑与博弈论息息相关。

博弈的定义
根据定义,博弈是在一定的规则下,各个参与者根据掌握的信息,决定自己的行动策略,以实现利益最大化或是风险最小化。
博弈论起源于运筹学和经济学,更像是数学和社会科学的结合体,因此社会/经济中的很多现象都可以用博弈论进行解释。此外生物学中也会用博弈论来预测生物的进化。
博弈四要素
参与者/玩家(Player):博弈中的每个参与者被称为玩家,每个玩家都有自己的目标和策略。
策略(Strategies):策略即玩家可以采取的行动。
支付(Payoffs):支付是玩家在策略组合中的收益和损失。
信息(Infomation):信息是玩家进行决策时获得的信息。
博弈的分类
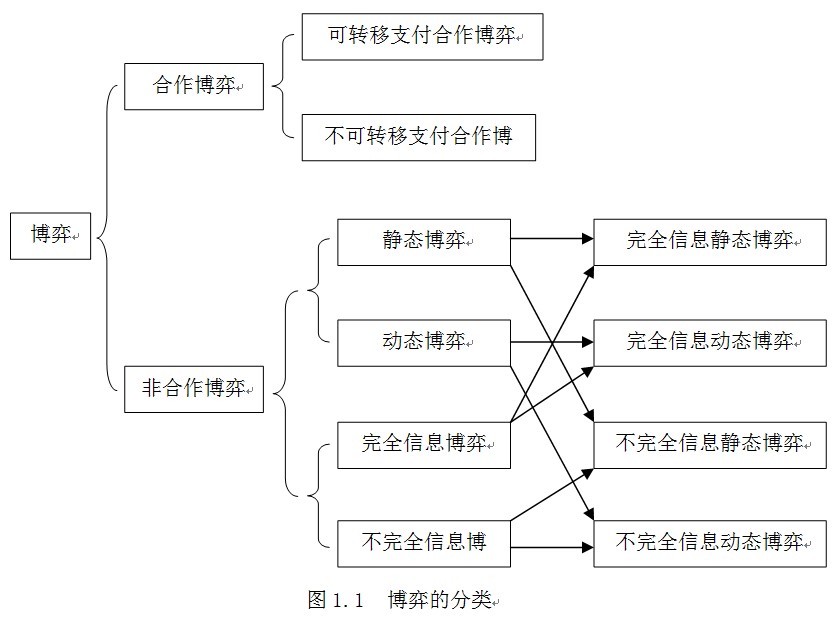
博弈的分类主要可以从三个维度来看,分别是是否合作,行动顺序,玩家的信息水平:
- 合作博弈:玩家之间是否有一个具有约束力的协议/规则。
- 行动顺序:玩家的决策是否有时间顺序。
- 信息水平:玩家对于其他玩家的了解程度。
| 信息/行动顺序 | 静态(玩家同时行动/彼此不知道行动) | 动态(玩家行动由先后顺序) |
|---|---|---|
| 完全信息 | 完全信息静态博弈(纳什均衡) | 完全信息动态博弈(子博弈完美纳什均衡) |
| 不完全信息 | 不完全信息静态博弈(贝叶斯纳什均衡) | 不完全信息动态博弈(完美贝叶斯纳什均衡) |
博弈的数学定义
博弈可以被抽象为范式,比较典型的有以下几个:
博弈的玩家集可以表示为 $N={1,2,…,n}$
每个玩家的策略集表示为 $S_{i},\forall i\in N$
每个玩家的支付集表示为 $R_{i},\forall i\in N$
因此,一个静态博弈可以表示为 $\left.v=\langle N,{S_{i}},{R_{i}}\right\rangle$
此外,还有一种定义:
设定${N}$是玩家的集合,每个玩家$i\in\mathbb{N};$都有一个策略集合:
$\pi : \prod_{i \in \mathbb{N}} i \to \mathbb{R}^{\mathbb{N}}$
也就是说,只要知道玩家的策略集合,就可以找到一个对应的实数。
TCP Backoff游戏和收益矩阵
斯坦福大学的博弈论课程中以一个TCP backoff机制作为引子介绍了博弈论。
这是计算机网络中的退避协议,用来处理网络拥堵时的流量分配。两台电脑之间想要实现通信,可以选择建立回退机制以及不建立回退机制。如果AB双方均建立回退机制,则双方延迟都是1。如果A、B一方建立回退机制,另一方不建立,那么建立的一方延迟是4,不建立的一方延迟是0。如果双方都不建立回退机制,则双方延迟都是3。
根据这种规则,可以构建一个矩阵如下:
| B / A | Y | N |
|---|---|---|
| Y | (-1,-1) | (-4,0) |
| N | (0,-4) | (-3,3) |
上面这个矩阵被称为收益矩阵,在博弈论中起到了重要的作用。A/B的不同选择带来的收益,将由一个实数进行表示。
今天先写到这,下次再继续写。
2023/12/30 于苏州